Critical value: Definition, Formula, Importance, and Examples
The critical value is derived from the level of significance (α) and the degrees of freedom (df) of the test. When it is actually true the level of significance is the probability of rejecting the null hypothesis, and it is typically set at 0.01 or 0.05. The degrees of freedom refers to the number of independent observations in the sample used for the test.
In this article, we will discuss the definition of critical value, formulas of critical values, confidence interval, and classification of critical value. Also with the help of examples, the topic will be explained.
Critical value
In statistics, a critical value is a value that is used to determine the rejection or acceptance of a null hypothesis in a hypothesis test. It is an essential concept in hypothesis testing and helps to determine the statistical significance of the results obtained.
The null hypothesis is not rejected if the test statistic, which is derived from the sample data, falls inside the acceptance range. If the test statistic falls within the rejection region, which is determined by the critical value, it is concluded that there is sufficient evidence to support the alternative hypothesis, and the result of the null hypothesis is rejected.
Critical value Formula
The formula for the critical value depends on the specific statistical test being conducted. In general, critical values are determined using tables or statistical software and are based on the level of significance and degrees of freedom for the test.
For example, the critical value for a t-test with n degrees of freedom at a significance level of α can be calculated as:
T critical = t (α/2, n-1)
where t (α/2, n-1) is the t-value obtained from a t-distribution table with a given level of significance (α) and degrees of freedom (n-1). The critical value can also be calculated for other statistical tests, such as the F-test or chi-squared test, using their respective formulas and tables.
What is a confidence interval in critical value?
A confidence interval is a range of values, which depends on a critical value. It is often set to 95%, which means that there is a 95% chance that the true parameter lies within the calculated interval.
Critical value: classification
- Z-critical value: The z critical value is used in hypothesis tests and confidence intervals when the population standard deviation is known, or the sample size is large enough to assume normality. The z-critical value is found by looking up the corresponding value in the standard normal distribution table.
- T-critical value: The t-critical value used when population standard deviation is unknown in this case the hypothesis tests and confidence intervals the sample size is small. The t-critical value depends on the degrees of freedom (df) and the level of significance and can be found using a t-distribution table.
- F-critical value: The F-critical value is used in ANOVA (analysis of variance) tests to compare the means of three or more groups. The F-critical value depends on the degrees of freedom for the numerator and denominator, and the level of significance. Or F-distribution table also shows the F-critical value.
- Chi-square critical value: The chi-square critical value is used in chi-square tests for goodness of fit and independence. The chi-square critical value depends on the degrees of freedom and the level of significance and can be found using a chi-square distribution table.
In general, when the observed test statistic is statistically significant or not critical values critical value is used whether by comparing it to the corresponding critical value from the appropriate distribution.
Steps to find the critical value
Here we discuss the step-by-step guide on how to calculate the critical value for a statistical test:
Step 1: Determine the level of significance (α) for the test, which represents the probability of rejecting the null hypothesis when it is actually true. This is typically set to 0.05 or 0.01 for most tests.
Step 2: Determine the degrees of freedom (df) for the test, which depends on the sample size and the type of test being conducted. For example, a t-test with a sample size of n and two groups would have df = 2n – 2.
Step 3: Determine the type of distribution to use for the test, which depends on the sample size and the assumptions made about the population. For example, a t-distribution is used for small sample sizes when the population standard deviation is unknown, while a z-distribution is used for large sample sizes or when the population standard deviation is known.
Step 4: Look up the critical value from a table of critical values or use a statistical calculator to find the critical value. The critical value depends on the level of significance, degrees of freedom, and type of distribution being used for the test.
Examples of critical value
Example 1:
Suppose we want to calculate the T-critical value for a two-tailed test with a sample size of 10 and a 95% confidence level.
Answer:
Step 1: Determine the level of significance (α) for the test, the confidence level is:
0.05 for a 95%.
Step 2: Determine the degrees of freedom (df) for the test:
df = n – 1 = 10 – 1 = 9
Step 3: Look up the T-critical value from a T-distribution table:
Using a T-distribution table, with 9 degrees of freedom and a 0.025 (2-tailed) significance level, we find the T-critical value to be approximately 2.262.
This means that if the calculated T-statistic for the test exceeds ±2.262, At a 95% confidence level we can reject the null hypothesis.
Example 2:
Suppose we have a sample of 30 observations, and we want to test whether the sample mean is significantly different from the population mean at a 95% confidence level
Solution:
Step 1: Determine the level of significance (α) for the test, the confidence level is:
0.05 for a 95%.
Step 2: Determine the degrees of freedom (df) for the test, which is:
n-1 = 29 in this case.
Step 3: Determine the type of distribution to use for the test, which is a t-distribution since the population standard deviation is unknown.
Step 4: Look up the t-critical value from the t-distribution table using the level of significance and degrees of freedom. T-critical value is 2.045 for a two-tailed test at a 95% confidence level. A t table calculator can also be used to find t critical value with table.
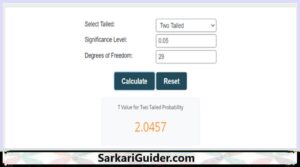
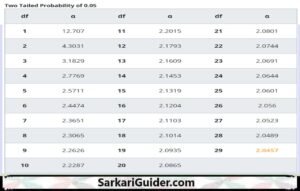Step 5: In this step standard error of the mean and sample mean. Suppose the sample mean is 25 and the sample standard deviation is 5 and the. Then the standard error of the mean is calculated as s/√n = 5/√30 = 0.912.
Step 6: Calculate the t-statistic using the formula t = (x̄ – μ) / (s/√n), where x̄ is the sample mean, μ denotes the population means, s denotes the sample standard deviation, and n denotes the sample size. In this case, the t-statistic is (25 – μ) / 0.912.
Frequently asked question
Question 1:
The method critical value determined?
Answer:
A critical value is determined based on the chosen significance level, the distribution of the test statistic, and the degrees of freedom. It can be found using a table or a calculator.
Question 2:
To find the critical values what are some common distributions used to find critical values?
Answer:
Some common distributions used to find critical values include the normal distribution, t-distribution, F-distribution, and chi-square distribution.
Question 3:
What is the relationship between the critical value and the p-value?
Answer:
The critical value is used to determine the cut-off point for rejecting or not rejecting the null hypothesis. The p-value, on the other hand, is a probability that represents the likelihood of observing the data or more extreme data, assuming the null hypothesis is true.
Summary
In this article, we have discussed the definition of critical value, formulas of critical values, confidence interval, and classification of critical value. Also with the help of examples, the topic will be explained. After complete studying this article anyone can defend this article easily.
Disclaimer: sarkariguider.com is created only for the purpose of education and knowledge. sarkariguider.com does not own these book/materials, neither created nor scanned. We provide the links which is already available on the internet. For any quarries, Disclaimer are requested to kindly contact us, we assured you we will do our best. We do not support piracy, this copy was provided for students who are financially troubled but deserving to learn. If in any way it violates the law or there is a problem, please mail us- sarkariguider@gmail.com
